Curve

Description

When selecting the Curve option () inside the Segment Type frame, you will be presented with the panel shown in the image below. Note that the options common to all curve types have been discussed in the Draw Curves landing page. Here, we will discuss only the options that are unique to the Curve segment type.

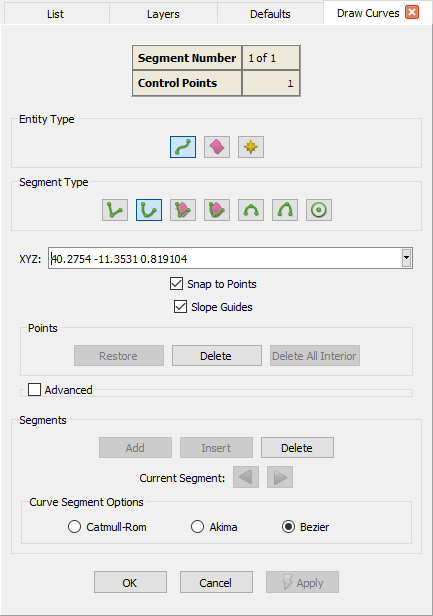
Curve segments can be created freely in three dimensional space and are cubic polynomials between successive points. Their slope is defined either by a Catmull-Rom, Akima, or Bezier control algorithm. Choose which slope control is used in the Curve Segment Options frame.

• Catmull-Rom: The slope at a given point is parallel to a chord between the two adjacent points. At the end of a curve, the slope will be tangent to the end point and the adjacent point.
• Akima: The slope at a given point uses a stencil of five consecutive points and produces curves with fewer “wiggles” or overshoot. One result of the five point stencil is that three consecutive points which lie on a line will have linear slope between them.
• Bezier: Allows slope control at each control point. The slope must remain continuous. If a slope discontinuity is desired, a new segment must be started at the location of the discontinuity. This is the only curve segment type that makes the Slope Guides checkbox (explained below) become enabled.

When the Bezier curve segment type is selected, the Slope Guides option allows you to ensure that the curve being created is tangent/orthogonal to an existing curve or normal to a database surface. With the option checked on, the slope at any control point shared between the new curve and an existent curve, can be adjusted to make the new curve either tangent or orthogonal to the existent curve at that point. Additionally, if the existent curve sharing a control point is constrained to an underlying database surface, the new curve could also be made normal to the surface at that point.

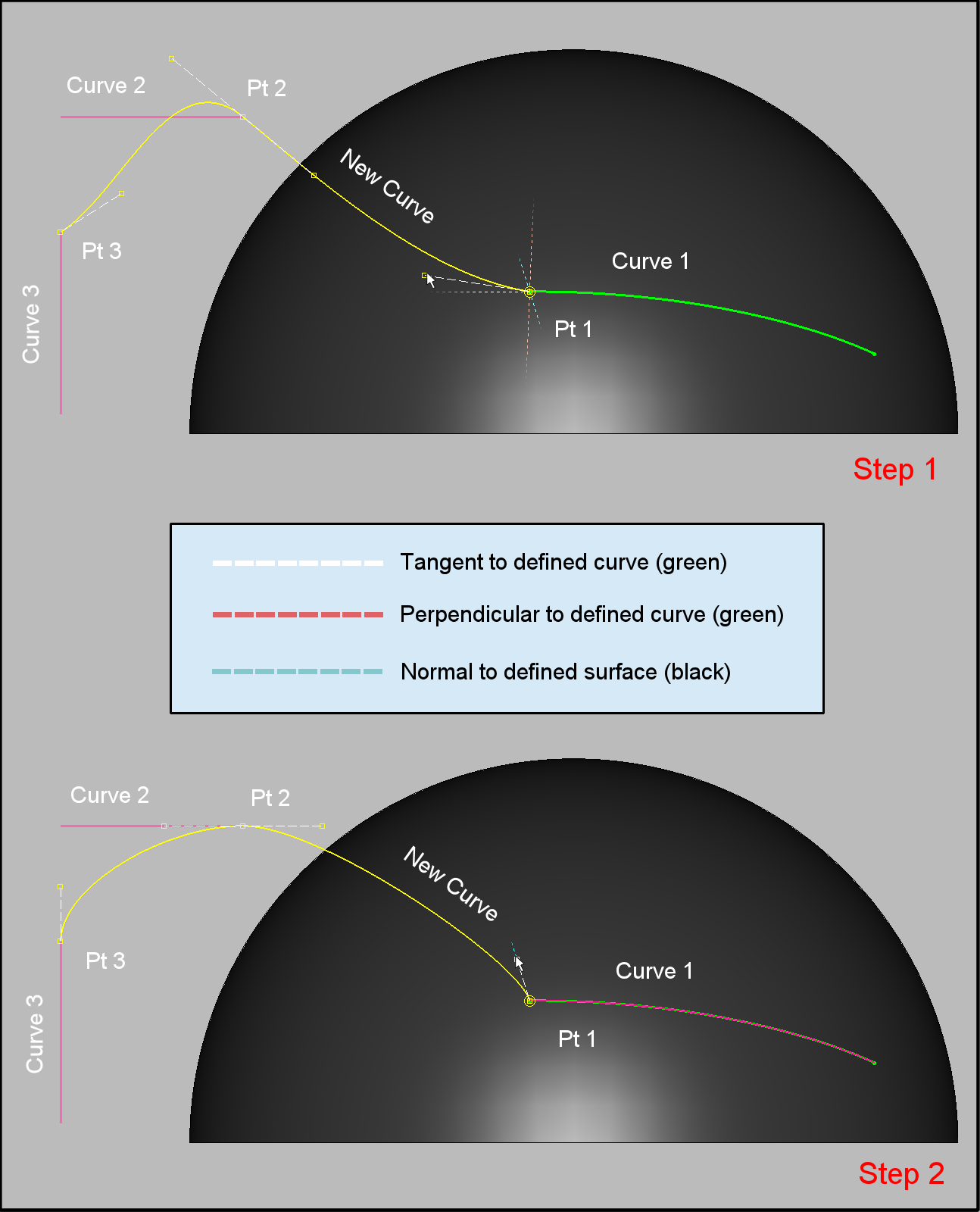
In order to adjust the slope of the new Bezier curve at a shared control point, simply select and drag the slope handles as shown in the image below. Note that slope guides tangent and orthogonal to the existent curve at the shared point's location will be shown in the Display window. Moreover, in the case of an existent curve that is constrained to a database surface, an additional guide normal to the surface at the shared point's location will also be shown. The guides are color-coded broken lines (see image below). Dragging the slope handles near the proximity of one of the guides will lock the cursor motion in the preferred location and highlight the entity providing the selected slope.

In the image below, a new Bezier curve (New Curve shown in yellow) has three control points shared with other existing curves (Curve 1, Curve 2, and Curve 3); one of the existing curves is constrained to an underlying database surface. The top portion of the image (Step 1) shows the initial state of the new curve before its slope at the shared control points is adjusted. The lower portion (Step 2), shows the final curve being normal to the database surface at the control point Pt1, tangent to the Curve 2 at point Pt 2, and tangent to the Curve 3 at Pt 3.

Demonstration

Creating Curves

Curve Slope Continuity